Abstract

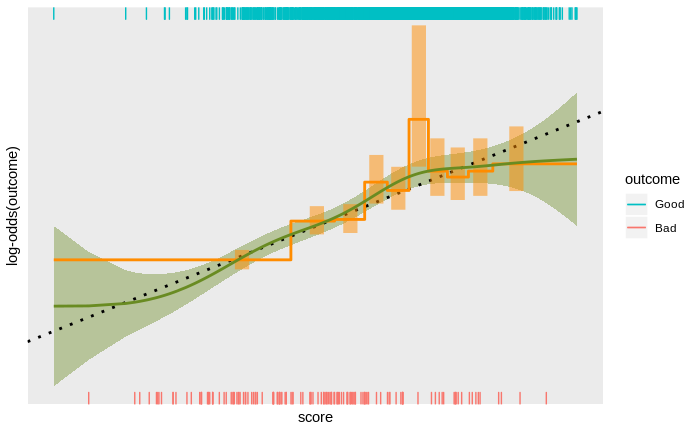
Score calibration is the process of empirically determining the relationship between a score and an outcome on some population of interest, and scaling is the process of expressing that relationship in agreed units. Calibration is often treated as a simple matter and attacked with simple tools – typically, either assuming the relationship between score and log-odds is linear and fitting a logistic regression with the score as the only covariate, or dividing the score range into bands and plotting the empirical log-odds as a function of score band.

Both approaches ignore some information in the data. The assumption of a linear score to log-odds relationship is too restrictive and score banding ignores the continuity of the scores. While a linear score to log-odds relationship is often an adequate approximation, the reality can be much more interesting, with noticeable deviations from the linear trend. These deviations include large-scale non-linearity, small-scale non-monotonicity, discrete discontinuities, and complete breakdown of the linear trend at extreme scores.

Detecting these effects requires a more sophisticated approach to empirically determining the score to outcome relationship. Taking a more sophisticated approach can be surprisingly tricky: the typically strong linear trend can obscure smaller deviations from linearity; detecting subtle trends requires exploiting the continuity of the scores, which can obscure discrete deviations; trends at extreme scores (out in the data-sparse tails of the distribution of scores) can be obscured by trends at less extreme scores (where there is more data); score distributions with some specific values that are relatively common can disrupt methods relying on continuity; and any modelling technique can introduce its own biases.

Over the years I have developed a personal approach to these issues in score calibration and implemented them as an open source, publicly accessible R package for score calibration. I discuss these technical issues in empirical score calibration and show how they are addressed in the scorecal package.