Publications
Filter by type:
Commentaries on 'Learning Sensorimotor Control with Neuromorphic Sensors: Toward Hyperdimensional Active Perception' [Science Robotics Vol. 4 Issue 30 (2019) 1-10]
VSA, Analogy, and Dynamic Similarity
Similarity (the angle between vectors) is central to the mechanics of VSA/HDC. Introductory papers (e.g. [8]) necessarily devote space to vector similarityand the effect of the primitive operators (sum, product, permutation) on similarity. Most VSA examples rely on static similarity, where the vector representations are fixed over the time scale of the core computation (which is usually a single-pass, feed-forward computation). This emphasises encoding methods (e.g. [12, 13]) that create vector representations with the similarity structure required by the core computation. Random Indexing [13] is an instance of the vector embedding approach to representation [11] that is widely used in NLP and ML. The important point is that the vector embeddings are developed in advance and then used as static representations (with fixed similarity structure) in the subsequent computation of interest.
Human similarity judgments are known to be context-dependent (see [3] for a brief review). It has also been argued that similarity and analogy are based on the same processes [6] and that cognition is so thoroughly context-dependent that representations are created on-the-fly in response to task demands [2]. This seems extreme, but doesn’t necessarily imply that the base representations are context-dependent as long as the cognitive process that compares them is context-dependent, which can be achieved by having dynamic representations that are derived from the static base representations by context-dependent transforms (or any functionally equivalent process).
An obvious candidate for a dynamic transformation function in VSA is substitution by binding, because the substitution can be specified as a vector and dynamically generated (see Representing substitution with a computed mapping in [8]). This implies an internal degree of freedom (a register to hold the substitution vector while it evolves) and a recurrent VSA circuit to provide the dynamics to evolve the substitution vector.
These essential aspects are present in [4], which finds the maximal subgraph isomorphism between two graphs represented as vectors. This is implemented as a recurrent VSA circuit with a register containing a substitution vector that evolves and settles over the course of the computation. The final state of the substitution vector represents the set of substitutions that transforms the static base representation of each graph into the best subgraph isomorphism to the static base representation of the other graph. This is a useful step along the path to an analogical memory system.
Interestingly, the subgraph isomorphism circuit can be interpreted as related to the recently developed Resonator Circuits for factorisation of VSA representations [9], which have internal degrees of freedom for each of the factors to be calculated and a recurrent VSA dynamics that settles on the factorisation. The graph isomorphism circuit can be interpreted as finding a factor (the substitution vector) such that the product of that factor with each of the graphs is the best possible approximation to the other graph. This links the whole enterprise back to statistical modelling, where there is a long history of approximating matrices/tensors as the product of simpler factors [10].
References
1. Blokpoel, M., Wareham, T., Haselager, P., van Rooij, I.: Deep Analogical Inference as the Origin of Hypotheses. The Journal of Problem Solving 11(1), 1–24 (2018)
2. Chalmers, D.J., French, R.M., Hofstadter, D.R.: High-level perception, representation, and analogy: A critique of artificial intelligence methodology. Journal of Experimental & Theoretical Artificial Intelligence 4(3), 185–211 (1992)
3. Cheng, Y.: Context-dependent similarity. In: Proceedings of the Sixth Annual Conference on Uncertainty in Artificial Intelligence (UAI’90), pp. 27–30. Cambridge, MA, USA (1990)
4. Gayler, R.W., Levy, S.D.: A distributed basis for analogical mapping. In: Proceedings of the Second International Conference on Analogy (ANALOGY-2009), pp. 165–174. New Bulgarian University, Sofia, Bulgaria (2009)
5. Gentner, D.: Structure-mapping: A theoretical framework for analogy. Cognitive Science 7(2), 155–170 (1983)
6. Gentner, D., Markman, A.B.: Structure mapping in analogy and similarity. American Psychologist 52(1), 45–56 (1997)
7. Gust, H., Krumnack, U., Kühnberger, K.-U., Schwering, A.: Analogical Reasoning: A core of cognition. KI - Künstliche Intelligenz 1(8), 8–12 (2008)
8. Kanerva, P.: Hyperdimensional computing: An introduction to computing in distributed representation with high-dimensional random vectors. Cognitive Computation 1, 139–159 (2009)
9. Kent, S.J., Frady, E.P., Sommer, F.T., Olshausen, B.A.: Resonator Circuits for factoring high-dimensional vectors. http://arxiv.org/abs/1906.11684 (2019)
10. Kolda, T.G., Bader, B.W.: Tensor decompositions and applications. SIAM Review 51(3), 455–500 (2009)
11. Pennington, J., Socher, R., Manning, C.D.: GloVe: Global vectors for word representation. In: Proceedings of the 2014 Conference on Empirical Methods in Natural Language Processing (EMNLP), pp. 1532–1543. Association for Computational Linguistics, Doha, Qatar (2014)
12. Purdy, S.: Encoding data for HTM systems. http://arxiv.org/abs/1602.05925 (2016)
13. Sahlgren, M.: An introduction to random indexing. In: Proceedings of the Methods and Applications of Semantic Indexing Workshop at the 7th International Conference on Terminology and Knowledge Engineering (TKE 2005), Copenhagen, Denmark (2005)
Connecting Twenty-First Century Connectionism and Wittgenstein
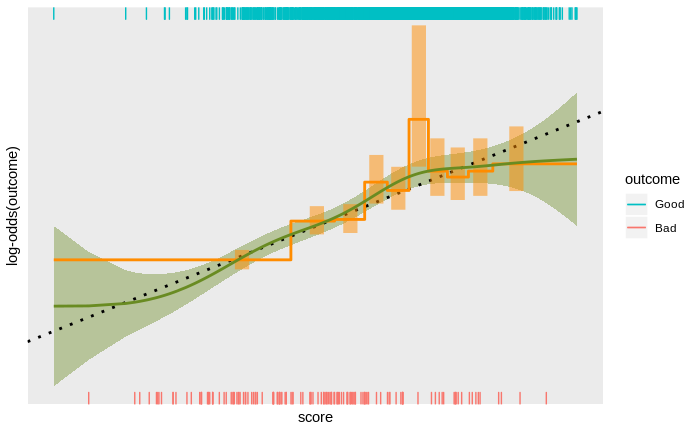
scorecal - Empirical score calibration under the microscope
Score calibration is the process of empirically determining the relationship between a score and an outcome on some population of interest, and scaling is the process of expressing that relationship in agreed units. Calibration is often treated as a simple matter and attacked with simple tools – typically, either assuming the relationship between score and log-odds is linear and fitting a logistic regression with the score as the only covariate, or dividing the score range into bands and plotting the empirical log-odds as a function of score band.
Both approaches ignore some information in the data. The assumption of a linear score to log-odds relationship is too restrictive and score banding ignores the continuity of the scores. While a linear score to log-odds relationship is often an adequate approximation, the reality can be much more interesting, with noticeable deviations from the linear trend. These deviations include large-scale non-linearity, small-scale non-monotonicity, discrete discontinuities, and complete breakdown of the linear trend at extreme scores.
Detecting these effects requires a more sophisticated approach to empirically determining the score to outcome relationship. Taking a more sophisticated approach can be surprisingly tricky: the typically strong linear trend can obscure smaller deviations from linearity; detecting subtle trends requires exploiting the continuity of the scores, which can obscure discrete deviations; trends at extreme scores (out in the data-sparse tails of the distribution of scores) can be obscured by trends at less extreme scores (where there is more data); score distributions with some specific values that are relatively common can disrupt methods relying on continuity; and any modelling technique can introduce its own biases.
Over the years I have developed a personal approach to these issues in score calibration and implemented them as an open source, publicly accessible R package for score calibration. I discuss these technical issues in empirical score calibration and show how they are addressed in the scorecal package.
VSA: Vector Symbolic Architectures for Cognitive Computing in Neural Networks
Comment: Classifier Technology and the Illusion of Progress — Credit Scoring
Vector Symbolic Architectures answer Jackendoff's challenges for cognitive neuroscience
Signal Detection for Credit Scoring Practitioners
The ROC curve is useful for assessing the predictive power of risk models and is relatively well known for this purpose in the credit scoring community. The ROC curve is a component of the Theory of Signal Detection (TSD), a theory which has pervasive links to many issues in model building. However, these conceptual links and their associated insights and techniques are less well known than they deserve to be among credit scoring practitioners.
The purpose of this paper is to alert credit risk modelers to the relationships between TSD and common scorecard development concepts and to provide a toolbox of simple techniques and interpretations.